ロトカ・ボルテラ方程式とは、捕食生物および被捕食生物の個体数変動を
数式化した方程式であり、1階の二元連立微分方程式の代表的な問題です。
この方程式を解く際もRunge－Kutta法が大活躍します。具体的な方法論については
ゴッドフット企画さまのHPを引用させていただきます。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
引用元：http://homepage1.nifty.com/gfk/rungekutta.htm
次の１階２元連立微分方程式で説明する。

　dφ/dt = F( t , φ, ω)
　dω/dt = G( t , φ, ω)

　F,Gは時間tと変数φ、ωの関数

初期値　t=t0　の時、φ=φ0, ω=ω0とすると、Δt後の変数値は下式となる。

　　k1 = Δt・F( t0, φ0, ω0)
　　m1 = Δt・G( t0, φ0, ω0)

　 k2 = Δt・F( t0+Δt/2, φ0+k1/2, ω0+m1/2)
　　m2 = Δt・G( t0+Δt/2, φ0+k1/2, ω0+m1/2)

　　k3 = Δt・F( t0+Δt/2, φ0+k2/2, ω0+m2/2)
　　m3 = Δt・G( t0+Δt/2, φ0+k2/2, ω0+m2/2)

　　k4 = Δt・F( t0+Δt, φ0+k3, ω0+m3)
　　m4 = Δt・G( t0+Δt, φ0+k3, ω0+m3)

　　k = (k1+2・K2+2・k3+k4)/6
　　m = (m1+2・m2+2・m3+m4)/6

Δt後の変数値φ1,ω1は

　　φ1 = φ0 + k
　　ω1 = ω0 + m

となる。

この手続きを繰り返せば、離散的だが、すべての時間での変数値が求まります。
ちなみに、Δtは0.0001秒のような微小値を設定する必要があります。
Δtが大きすぎると解が発散する場合があります。

計算量が多いので、手計算は困難です。EXCELなどを使って計算しましょう。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

このゴットフット企画さまのHPの理論を応用すれば、ロトカ・ボルテラ方程式の
解析コードが作成できます。そこで、方程式例として
dx/dt = (8 - 3 * y) * x
dy/dt = (-18 + 4 * x) * y　
初期条件t = 0, x = 10 , y = 7
を考えましょう。この微分方程式の数値計算用プログラミングのソースコードを
下記に記します。

Sub RungeKutta()

Dim t, dt As Single
Dim x, y As Single
Dim K1, K2, K3, K4 As Single
Dim L1, L2, L3, L4 As Single
Dim i As Long

'初期値の入力

t = 0
x = 10#
y = 7#
dt = 0.01

Cells(1, 1).Value = "t"
Cells(1, 2).Value = "x"
Cells(1, 3).Value = "y"

Cells(2, 1).Value = t
Cells(2, 2).Value = x
Cells(2, 3).Value = y

For i = 0 To 5000

K1 = F(t, x, y) * dt
L1 = G(t, x, y) * dt

K2 = F(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
L2 = G(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt

K3 = F(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
L3 = G(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt

K4 = F(t + dt, x + K3, y + L3) * dt
L4 = G(t + dt, x + K3, y + L3) * dt

t = t + dt
x = x + (K1 + 2 * K2 + 2 * K3 + K4) / 6
y = y + (L1 + 2 * L2 + 2 * L3 + L4) / 6

Cells(3 + i, 1).Value = t
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y

Next i

End Sub

Function F(t, x, y)

F = (8 - 3 * y) * x

End Function

Function G(t, x, y)

G = (-18 + 4 * x) * y

End Function

解析結果：



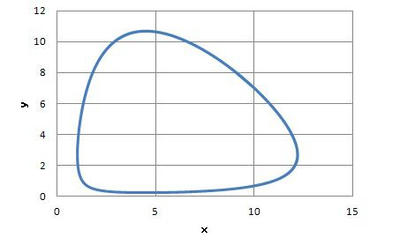
※特定のxに対してyは周期的に変化していることが確認できる。



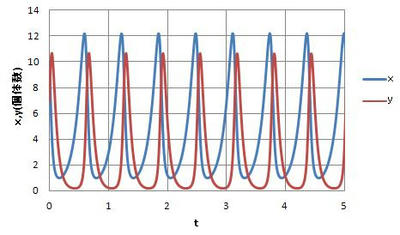
※ｘ、yの経時変化をみると図のようになっている。

このようにして、Runge-Kutta法を応用すると連立微分方程式のような
複雑な方程式も解析できます。

[3回]

Runge-Kutta法とは、微分方程式の解法の一つです。
(原理の詳細：http://hooktail.org/computer/index.php?Runge-Kutta%CB%A1)
例えば、任意の微分方程式に対して、

dy/dx = f(x,y)に対して

k1 = f(x,y)
k2 = f(x+Δx/2,y+k1*Δx/2)
k3 = f(x+Δx/2,y+k2*Δx/2)
k4 = f(x+Δx,y+k3*Δx)
Δy = (Δx/6)*(k1+2k2+2k3+k4)

とすることでΔxに対するΔyを予想し、y=f(x)を正確に近似する方法です。

具体的にExcelのマクロを作って計算してみましょう。

問い:微分方程式dy/dx = xyをRunge-Kutta法で解け。ただし、x = 0ならy=10とする。

解法：上記計算のルールを用いてマクロをつくると下のようになる。

Sub RungeKutta()

Dim K1, K2, K3, K4 As Single
Dim x, y As Single
Dim dx, dy As Single
Dim i As Long

Cells(2, 2).Value = "x"
Cells(2, 3).Value = "y"

x = 0
y = 10
Cells(3, 2).Value = x
Cells(3, 3).Value = y
dx = 0.01

For i = 1 To 300

K1 = F(x, y)
K2 = F(x + dx / 2, y + dx / 2 * K1)
K3 = F(x + dx / 2, y + dx / 2 * K2)
K4 = F(x + dx, y + dx * K3)
dy = (K1 + 2 * K2 + 2 * K3 + K4) * (dx / 6)
x = x + dx
y = y + dy
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y

Next i

End Sub

Function F(x, y)

F = -2 * x * y

End Function

計算結果


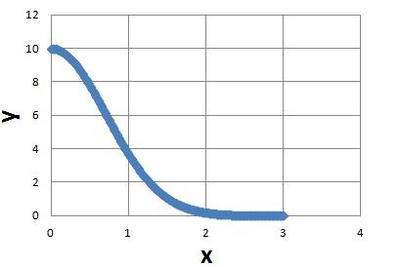
このような簡素なプログラミングでも微分方程式は精度よく計算できます。
とくに、Runge-Kutta法は常微分方程式であれば、
複雑な式でも解析が容易です。以後、Runge-Kutta法の解析例を
紹介していきたいと思います。

[6回]

前回、溶媒の粘度をη0、溶液の粘度をηとして、
オストワルドの粘度計の原理を示した。

今日は固有粘度について語ろうと思う。

溶液の溶質の濃度をCとすると、実はηとη0の間には、一般的に

η = η0(1+[η]C+[η2]C^2+…)…(1)

が成り立ち、状態方程式をビリアル展開した式に似た近似式が成り立つ。

よって、高分子溶液のようにCが十分に小さい場合、
C^2<<1なので、C^2≒0と近似してよい。この場合、

η = η0(1+[η]C)⇔[η]= {(η-η0)/η0}/C より[η]は次式のようになる。

∴　[η]　 =　Lim{C⇒0}　(η/η0 - 1)/C　…(2)

このような[η]のことを固有粘度と呼ぶ。
固有粘度は、Huggins Plotというデータ解析で解析することができる。

これは、Cに対して(η/η0-1)/Cをプロットすることで固有粘度を解析する方法である。

例えば、下表にEXCELでポリスチレン-トルエン溶液を用いて
(η/η0-1)/Cを解析した例を記す。



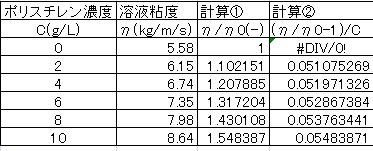
この表に対して、ポリスチレン濃度と計算②をプロットしたものがHuggins Plotであり、
Excelでグラフ化すると図のようになる。



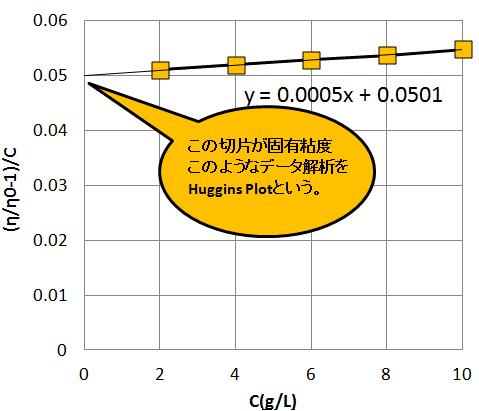
グラフの切片は、Lim{C⇒0}　(η/η0 - 1)/Cと同じであり、

固有粘度[η]は、[η]=0.0501となっていることが確認できた。

実験的にはこのようにして固有粘度を求められる。

[9回]

趣味の勉強日記です。

オストワルドの粘度計とは、下記動画で紹介されているガラス器具であり、
Ostwald　viscometerともいいます。



この器具は、溶液の粘度測定で幅広く利用されます。
英語で何を言ってるか分からない方のために図を用意しました。
詳細は下記をご覧ください。



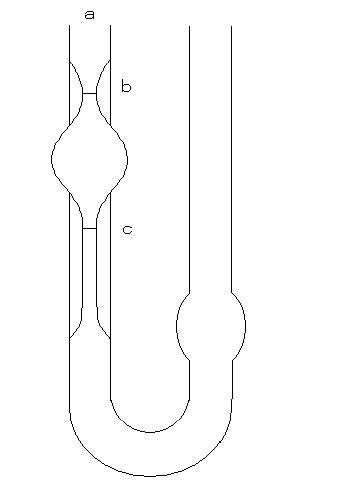
はじめに、右側から液体を入れます。注意してほしいのですが、
粘度測定を正確に行うなら恒温槽内で行いましょう。
次にa部にゴム管等をつけて溶液をb部まで吸い上げます。
温度が安定したところで、aを開放し液体を自由落下させます。
その際に液体がbからc部を通過する時間Δtをストップウォッチで測定することで
粘度を導くことが可能になるのです。なぜでしょうか？

はじめに、b部まで液体を吸い上げる際の圧力ΔPを計算しましょう。
このときの圧力変化ΔPは、ニュートンの運動方程式より導くことが可能であり、

ΔP = mg/S = ρgV/S = ρg(S・h)/S = ρgh…(1)
m…吸い上げた液体の質量
g…重力定数
S…bからc部までの平均断面積
V…bからc部の体積
h…bからc部までの高さ
ρ…液体の密度
となります。この流体の運動をハーゲンポアズイユの式で近似すると、

V/Δt = (πR^4/8η)*ΔP/h…(2)
を得ることができます。ここで、Rはb からcまでの容器断面における平均半径とします。(1)を(2)に代入すると、

η=(πρgR^4h)Δt/(8h)=ρAΔt　…(3)※A　= (πgR^4h)/(8h)であり定数

となり、粘度という物理量は非常にシンプルな関数で表現できました。

ふつう、溶媒の粘度をη0、溶液の粘度をηとして相対的に粘度を求めることが多いです。
なぜかというと、Aを決定しなくて済むからです。
上の式を考えればわかるけれども、溶媒の密度をρ0、落下時間をΔt0、
溶液の密度をρ、落下時間をΔtとすると

η0　=　A*ρ0*Δt0　…(4)
η　　=　A*ρ*Δt　…(5)
が導けます。(4)および(5)式からAを消去すると、

η/η0 = (ρ/ρ0)*(Δt/Δt0)…(6)

のような式を得ることができます。このη/η0 を相対粘度といいます。
オストワルドの粘度計は、このような相対粘度の解析に大変すぐれた
装置です。

[25回]

奇数を今度は次のように並べてみよう

1番目:1
2番目:3,5
3番目:7,9,11
4番目:13,15,17,19

規則性は理解できただろうか？
奇数列1,3,5,7,9,11,13,15,17,19…に対して
1番目の列は、奇数列の左から数字を1個取り出して1のみ
2番目の列は、先ほど取り出した1個を除き、奇数列の左から数字を2個取り出して3，5
…
といった具合で奇数を取り出しています。

前回と同じように、この和を見てみよう。

1番目:1 = 1 = 1×1×1
2番目:3+5 = 8 = 2×2×2
3番目:7+9+11 =27 = 3×3×3
4番目:13+15+17+19 = 64　=4×4×4
:
:
なんと、今度は3乗の数になっていました。
私は、このルールを発見した時、感動するとともに奇数は奇なる数と思いましたね。

この数列を利用して1^3+2^3+3^3+…+n^3を求めることが可能です。
n^3までの和は、1～n番目までの列に存在するすべての奇数の和と同じです。
また数列のルールにもどると、1からスタートして奇数列から
1+2+3+4+…+n個の奇数を取り出しています。
よってpart1より、奇数列の和は足した個数の二乗になるので
1^3+2^3+3^3+…+n^3　=(1+2+3+4+…+n)^2となることが容易に確認できるでしょう。

詳細：奇数を並べると-part1

こういう方法を用いても高校数学の数列の公式をつくることができるのです。

[1回]