ロトカ・ボルテラ方程式とは、捕食生物および被捕食生物の個体数変動を
数式化した方程式であり、1階の二元連立微分方程式の代表的な問題です。
この方程式を解く際もRunge－Kutta法が大活躍します。具体的な方法論については
ゴッドフット企画さまのHPを引用させていただきます。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
引用元：http://homepage1.nifty.com/gfk/rungekutta.htm
次の１階２元連立微分方程式で説明する。

　dφ/dt = F( t , φ, ω)
　dω/dt = G( t , φ, ω)

　F,Gは時間tと変数φ、ωの関数

初期値　t=t0　の時、φ=φ0, ω=ω0とすると、Δt後の変数値は下式となる。

　　k1 = Δt・F( t0, φ0, ω0)
　　m1 = Δt・G( t0, φ0, ω0)

　 k2 = Δt・F( t0+Δt/2, φ0+k1/2, ω0+m1/2)
　　m2 = Δt・G( t0+Δt/2, φ0+k1/2, ω0+m1/2)

　　k3 = Δt・F( t0+Δt/2, φ0+k2/2, ω0+m2/2)
　　m3 = Δt・G( t0+Δt/2, φ0+k2/2, ω0+m2/2)

　　k4 = Δt・F( t0+Δt, φ0+k3, ω0+m3)
　　m4 = Δt・G( t0+Δt, φ0+k3, ω0+m3)

　　k = (k1+2・K2+2・k3+k4)/6
　　m = (m1+2・m2+2・m3+m4)/6

Δt後の変数値φ1,ω1は

　　φ1 = φ0 + k
　　ω1 = ω0 + m

となる。

この手続きを繰り返せば、離散的だが、すべての時間での変数値が求まります。
ちなみに、Δtは0.0001秒のような微小値を設定する必要があります。
Δtが大きすぎると解が発散する場合があります。

計算量が多いので、手計算は困難です。EXCELなどを使って計算しましょう。
＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

このゴットフット企画さまのHPの理論を応用すれば、ロトカ・ボルテラ方程式の
解析コードが作成できます。そこで、方程式例として
dx/dt = (8 - 3 * y) * x
dy/dt = (-18 + 4 * x) * y　
初期条件t = 0, x = 10 , y = 7
を考えましょう。この微分方程式の数値計算用プログラミングのソースコードを
下記に記します。

Sub RungeKutta()

Dim t, dt As Single
Dim x, y As Single
Dim K1, K2, K3, K4 As Single
Dim L1, L2, L3, L4 As Single
Dim i As Long

'初期値の入力

t = 0
x = 10#
y = 7#
dt = 0.01

Cells(1, 1).Value = "t"
Cells(1, 2).Value = "x"
Cells(1, 3).Value = "y"

Cells(2, 1).Value = t
Cells(2, 2).Value = x
Cells(2, 3).Value = y

For i = 0 To 5000

K1 = F(t, x, y) * dt
L1 = G(t, x, y) * dt

K2 = F(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
L2 = G(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt

K3 = F(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
L3 = G(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt

K4 = F(t + dt, x + K3, y + L3) * dt
L4 = G(t + dt, x + K3, y + L3) * dt

t = t + dt
x = x + (K1 + 2 * K2 + 2 * K3 + K4) / 6
y = y + (L1 + 2 * L2 + 2 * L3 + L4) / 6

Cells(3 + i, 1).Value = t
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y

Next i

End Sub

Function F(t, x, y)

F = (8 - 3 * y) * x

End Function

Function G(t, x, y)

G = (-18 + 4 * x) * y

End Function

解析結果：



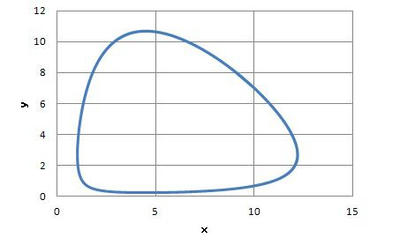
※特定のxに対してyは周期的に変化していることが確認できる。



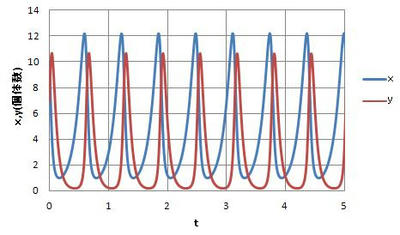
※ｘ、yの経時変化をみると図のようになっている。

このようにして、Runge-Kutta法を応用すると連立微分方程式のような
複雑な方程式も解析できます。

[3回]