Runge-Kutta法とは、微分方程式の解法の一つです。
(原理の詳細：http://hooktail.org/computer/index.php?Runge-Kutta%CB%A1)
例えば、任意の微分方程式に対して、

dy/dx = f(x,y)に対して

k1 = f(x,y)
k2 = f(x+Δx/2,y+k1*Δx/2)
k3 = f(x+Δx/2,y+k2*Δx/2)
k4 = f(x+Δx,y+k3*Δx)
Δy = (Δx/6)*(k1+2k2+2k3+k4)

とすることでΔxに対するΔyを予想し、y=f(x)を正確に近似する方法です。

具体的にExcelのマクロを作って計算してみましょう。

問い:微分方程式dy/dx = xyをRunge-Kutta法で解け。ただし、x = 0ならy=10とする。

解法：上記計算のルールを用いてマクロをつくると下のようになる。

Sub RungeKutta()

Dim K1, K2, K3, K4 As Single
Dim x, y As Single
Dim dx, dy As Single
Dim i As Long

Cells(2, 2).Value = "x"
Cells(2, 3).Value = "y"

x = 0
y = 10
Cells(3, 2).Value = x
Cells(3, 3).Value = y
dx = 0.01

For i = 1 To 300

K1 = F(x, y)
K2 = F(x + dx / 2, y + dx / 2 * K1)
K3 = F(x + dx / 2, y + dx / 2 * K2)
K4 = F(x + dx, y + dx * K3)
dy = (K1 + 2 * K2 + 2 * K3 + K4) * (dx / 6)
x = x + dx
y = y + dy
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y

Next i

End Sub

Function F(x, y)

F = -2 * x * y

End Function

計算結果


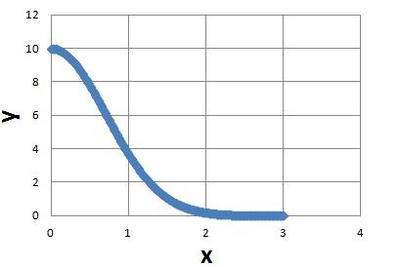
このような簡素なプログラミングでも微分方程式は精度よく計算できます。
とくに、Runge-Kutta法は常微分方程式であれば、
複雑な式でも解析が容易です。以後、Runge-Kutta法の解析例を
紹介していきたいと思います。

[6回]