前回、溶媒の粘度をη0、溶液の粘度をηとして、
オストワルドの粘度計の原理を示した。

今日は固有粘度について語ろうと思う。

溶液の溶質の濃度をCとすると、実はηとη0の間には、一般的に

η = η0(1+[η]C+[η2]C^2+…)…(1)

が成り立ち、状態方程式をビリアル展開した式に似た近似式が成り立つ。

よって、高分子溶液のようにCが十分に小さい場合、
C^2<<1なので、C^2≒0と近似してよい。この場合、

η = η0(1+[η]C)⇔[η]= {(η-η0)/η0}/C より[η]は次式のようになる。

∴　[η]　 =　Lim{C⇒0}　(η/η0 - 1)/C　…(2)

このような[η]のことを固有粘度と呼ぶ。
固有粘度は、Huggins Plotというデータ解析で解析することができる。

これは、Cに対して(η/η0-1)/Cをプロットすることで固有粘度を解析する方法である。

例えば、下表にEXCELでポリスチレン-トルエン溶液を用いて
(η/η0-1)/Cを解析した例を記す。



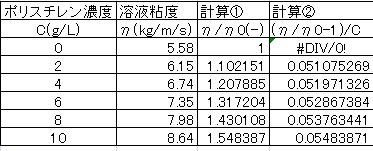
この表に対して、ポリスチレン濃度と計算②をプロットしたものがHuggins Plotであり、
Excelでグラフ化すると図のようになる。



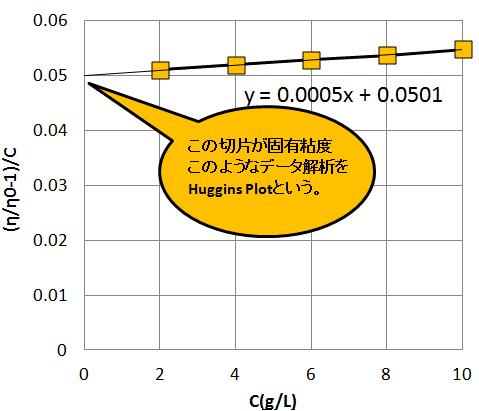
グラフの切片は、Lim{C⇒0}　(η/η0 - 1)/Cと同じであり、

固有粘度[η]は、[η]=0.0501となっていることが確認できた。

実験的にはこのようにして固有粘度を求められる。

[9回]