理系の若者が思ったことを書くブログです。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
素数とは、1 と自分自身以外に正の約数を持たない、1 でない自然数のことです。
1~100までの素数は容易に探索できるかもしれません。
でも1~1000までの素数となるとちょっと骨が折れるでしょうね。
そこで、プログラミングの出番です。
実を言うと素数を探索するアルゴリズムは複数あります。
したがって、素数はコンピュータ計算でも探索できます。
ここでは、次の方法で素数を探索してみようと思います。
① a_k = k (k = 1,2,3…1000)となる数列akを定義する。
② k = 1であれば、素数ではないと判断する。
③ k = 2であれば、素数と判断する。
③ k >2であるa_kを2~kまでのすべての数で割っていく。
④ ③のときに、割った数pに対してひとつでもa_k ≡ 0 (mod p) を満たせば
素数でないと判断する。
※modの意味がわからない方はこちらへ⇒http://sur.ac/faq/mod.html
⑤ kの値を繰り上げて③~④を繰り返す。
上の計算方法をVBAプログラムにすると次のようになります。
Sub primenumber()
Dim k, j As Long
Dim hantei As Long
Dim counter As Long
counter = 0
For k = 1 To 1000
If k = 1 Then
hantei = 0
'1は素数じゃない。
End If
If k = 2 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'2は素数である。
End If
If k = 3 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'3は素数である。
End If
If k > 3 Then
hantei = 1
For j = 2 To k - 1
Data = k Mod j
If Data = 0 Then
hantei = 0
End If
Next j
If hantei = 1 Then
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
End If
'3以上の数の素数判定実施。
End If
Next k
End Sub
解析結果:
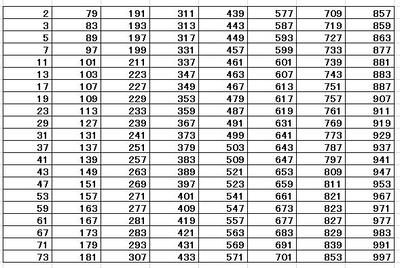
このように、プログラミングを勉強すれば素数も簡単に探せるようになるのです。
1~100までの素数は容易に探索できるかもしれません。
でも1~1000までの素数となるとちょっと骨が折れるでしょうね。
そこで、プログラミングの出番です。
実を言うと素数を探索するアルゴリズムは複数あります。
したがって、素数はコンピュータ計算でも探索できます。
ここでは、次の方法で素数を探索してみようと思います。
① a_k = k (k = 1,2,3…1000)となる数列akを定義する。
② k = 1であれば、素数ではないと判断する。
③ k = 2であれば、素数と判断する。
③ k >2であるa_kを2~kまでのすべての数で割っていく。
④ ③のときに、割った数pに対してひとつでもa_k ≡ 0 (mod p) を満たせば
素数でないと判断する。
※modの意味がわからない方はこちらへ⇒http://sur.ac/faq/mod.html
⑤ kの値を繰り上げて③~④を繰り返す。
上の計算方法をVBAプログラムにすると次のようになります。
Sub primenumber()
Dim k, j As Long
Dim hantei As Long
Dim counter As Long
counter = 0
For k = 1 To 1000
If k = 1 Then
hantei = 0
'1は素数じゃない。
End If
If k = 2 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'2は素数である。
End If
If k = 3 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'3は素数である。
End If
If k > 3 Then
hantei = 1
For j = 2 To k - 1
Data = k Mod j
If Data = 0 Then
hantei = 0
End If
Next j
If hantei = 1 Then
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
End If
'3以上の数の素数判定実施。
End If
Next k
End Sub
解析結果:
このように、プログラミングを勉強すれば素数も簡単に探せるようになるのです。
PR
PART1はあくまで台形公式についてのみ書きます。
今、y = x^2を0から1の範囲で積分せよという問題を考える。
この積分は簡単だと思う。何故なら、∫x^2dx =x^3/3+Cより、
1/3だとすぐ確認できるからである。
では、y=√(x^4-x+sinx)に変更するとどうだろうか?
こういう式になった途端にどうすればいいかわからなくなるだろう。
このように、数学的にちゃんと積分する方法がわからない式だってたくさんある。
しかし、y=f(x)がどんな式であれ、近似的に精度よく積分できる方法も存在する。
台形公式は、そういった手法の一つである。台形公式は、
積分範囲を何点かに分割して台形をつくり、その台形の面積を求めることで
数値積分する方法である。
具体例:今、y=f(x)をa~b( a
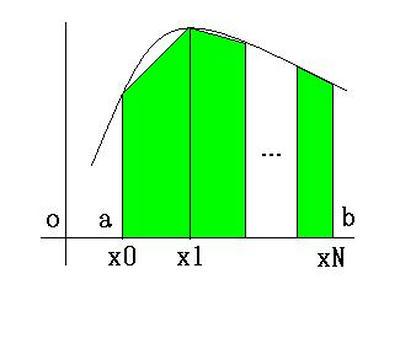
この図から台形の面積の総和Stを調べると、数学的に下記の式であらわせる。
St = {(f(x0)+f(x1))*(x1-x0)/2}+…+{(f(xN)+f(xN-1))*(xN-xN-1)/2}…(1)
今分割をx1-x0 = x2 - x1 = …xk+1-xk = xN - x0 = hとなるように行うのであれば、
St = {f(x0) + f(xN)}/2*h + Σf(xk)*h/2 (k=1 ~ k = N-1)…(2)
がなりたつ。分割数を増やしていけば、この台形の面積の総和は積分結果に近づく。
この(2)式を実行するプログラミングとf(x)を定義すれば、
どんな式でも簡単に積分できるようになるでしょう。
今、y = x^2を0から1の範囲で積分せよという問題を考える。
この積分は簡単だと思う。何故なら、∫x^2dx =x^3/3+Cより、
1/3だとすぐ確認できるからである。
では、y=√(x^4-x+sinx)に変更するとどうだろうか?
こういう式になった途端にどうすればいいかわからなくなるだろう。
このように、数学的にちゃんと積分する方法がわからない式だってたくさんある。
しかし、y=f(x)がどんな式であれ、近似的に精度よく積分できる方法も存在する。
台形公式は、そういった手法の一つである。台形公式は、
積分範囲を何点かに分割して台形をつくり、その台形の面積を求めることで
数値積分する方法である。
具体例:今、y=f(x)をa~b( a
この図から台形の面積の総和Stを調べると、数学的に下記の式であらわせる。
St = {(f(x0)+f(x1))*(x1-x0)/2}+…+{(f(xN)+f(xN-1))*(xN-xN-1)/2}…(1)
今分割をx1-x0 = x2 - x1 = …xk+1-xk = xN - x0 = hとなるように行うのであれば、
St = {f(x0) + f(xN)}/2*h + Σf(xk)*h/2 (k=1 ~ k = N-1)…(2)
がなりたつ。分割数を増やしていけば、この台形の面積の総和は積分結果に近づく。
この(2)式を実行するプログラミングとf(x)を定義すれば、
どんな式でも簡単に積分できるようになるでしょう。
ロトカ・ボルテラ方程式とは、捕食生物および被捕食生物の個体数変動を
数式化した方程式であり、1階の二元連立微分方程式の代表的な問題です。
この方程式を解く際もRunge-Kutta法が大活躍します。具体的な方法論については
ゴッドフット企画さまのHPを引用させていただきます。
=================================
引用元:http://homepage1.nifty.com/gfk/rungekutta.htm
次の1階2元連立微分方程式で説明する。
dφ/dt = F( t , φ, ω)
dω/dt = G( t , φ, ω)
F,Gは時間tと変数φ、ωの関数
初期値 t=t0 の時、φ=φ0, ω=ω0とすると、Δt後の変数値は下式となる。
k1 = Δt・F( t0, φ0, ω0)
m1 = Δt・G( t0, φ0, ω0)
k2 = Δt・F( t0+Δt/2, φ0+k1/2, ω0+m1/2)
m2 = Δt・G( t0+Δt/2, φ0+k1/2, ω0+m1/2)
k3 = Δt・F( t0+Δt/2, φ0+k2/2, ω0+m2/2)
m3 = Δt・G( t0+Δt/2, φ0+k2/2, ω0+m2/2)
k4 = Δt・F( t0+Δt, φ0+k3, ω0+m3)
m4 = Δt・G( t0+Δt, φ0+k3, ω0+m3)
k = (k1+2・K2+2・k3+k4)/6
m = (m1+2・m2+2・m3+m4)/6
Δt後の変数値φ1,ω1は
φ1 = φ0 + k
ω1 = ω0 + m
となる。
この手続きを繰り返せば、離散的だが、すべての時間での変数値が求まります。
ちなみに、Δtは0.0001秒のような微小値を設定する必要があります。
Δtが大きすぎると解が発散する場合があります。
計算量が多いので、手計算は困難です。EXCELなどを使って計算しましょう。
=================================
このゴットフット企画さまのHPの理論を応用すれば、ロトカ・ボルテラ方程式の
解析コードが作成できます。そこで、方程式例として
dx/dt = (8 - 3 * y) * x
dy/dt = (-18 + 4 * x) * y
初期条件t = 0, x = 10 , y = 7
を考えましょう。この微分方程式の数値計算用プログラミングのソースコードを
下記に記します。
Sub RungeKutta()
Dim t, dt As Single
Dim x, y As Single
Dim K1, K2, K3, K4 As Single
Dim L1, L2, L3, L4 As Single
Dim i As Long
'初期値の入力
t = 0
x = 10#
y = 7#
dt = 0.01
Cells(1, 1).Value = "t"
Cells(1, 2).Value = "x"
Cells(1, 3).Value = "y"
Cells(2, 1).Value = t
Cells(2, 2).Value = x
Cells(2, 3).Value = y
For i = 0 To 5000
K1 = F(t, x, y) * dt
L1 = G(t, x, y) * dt
K2 = F(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
L2 = G(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
K3 = F(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
L3 = G(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
K4 = F(t + dt, x + K3, y + L3) * dt
L4 = G(t + dt, x + K3, y + L3) * dt
t = t + dt
x = x + (K1 + 2 * K2 + 2 * K3 + K4) / 6
y = y + (L1 + 2 * L2 + 2 * L3 + L4) / 6
Cells(3 + i, 1).Value = t
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y
Next i
End Sub
Function F(t, x, y)
F = (8 - 3 * y) * x
End Function
Function G(t, x, y)
G = (-18 + 4 * x) * y
End Function
解析結果:
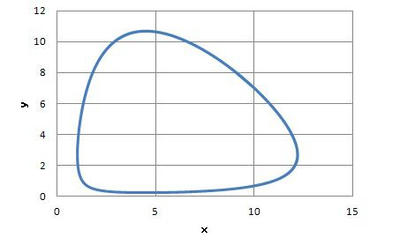
※特定のxに対してyは周期的に変化していることが確認できる。
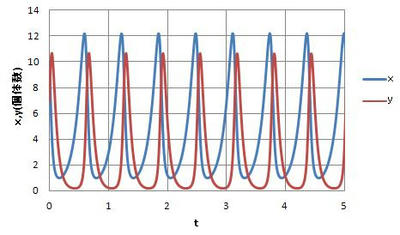
※x、yの経時変化をみると図のようになっている。
このようにして、Runge-Kutta法を応用すると連立微分方程式のような
複雑な方程式も解析できます。
数式化した方程式であり、1階の二元連立微分方程式の代表的な問題です。
この方程式を解く際もRunge-Kutta法が大活躍します。具体的な方法論については
ゴッドフット企画さまのHPを引用させていただきます。
=================================
引用元:http://homepage1.nifty.com/gfk/rungekutta.htm
次の1階2元連立微分方程式で説明する。
dφ/dt = F( t , φ, ω)
dω/dt = G( t , φ, ω)
F,Gは時間tと変数φ、ωの関数
初期値 t=t0 の時、φ=φ0, ω=ω0とすると、Δt後の変数値は下式となる。
k1 = Δt・F( t0, φ0, ω0)
m1 = Δt・G( t0, φ0, ω0)
k2 = Δt・F( t0+Δt/2, φ0+k1/2, ω0+m1/2)
m2 = Δt・G( t0+Δt/2, φ0+k1/2, ω0+m1/2)
k3 = Δt・F( t0+Δt/2, φ0+k2/2, ω0+m2/2)
m3 = Δt・G( t0+Δt/2, φ0+k2/2, ω0+m2/2)
k4 = Δt・F( t0+Δt, φ0+k3, ω0+m3)
m4 = Δt・G( t0+Δt, φ0+k3, ω0+m3)
k = (k1+2・K2+2・k3+k4)/6
m = (m1+2・m2+2・m3+m4)/6
Δt後の変数値φ1,ω1は
φ1 = φ0 + k
ω1 = ω0 + m
となる。
この手続きを繰り返せば、離散的だが、すべての時間での変数値が求まります。
ちなみに、Δtは0.0001秒のような微小値を設定する必要があります。
Δtが大きすぎると解が発散する場合があります。
計算量が多いので、手計算は困難です。EXCELなどを使って計算しましょう。
=================================
このゴットフット企画さまのHPの理論を応用すれば、ロトカ・ボルテラ方程式の
解析コードが作成できます。そこで、方程式例として
dx/dt = (8 - 3 * y) * x
dy/dt = (-18 + 4 * x) * y
初期条件t = 0, x = 10 , y = 7
を考えましょう。この微分方程式の数値計算用プログラミングのソースコードを
下記に記します。
Sub RungeKutta()
Dim t, dt As Single
Dim x, y As Single
Dim K1, K2, K3, K4 As Single
Dim L1, L2, L3, L4 As Single
Dim i As Long
'初期値の入力
t = 0
x = 10#
y = 7#
dt = 0.01
Cells(1, 1).Value = "t"
Cells(1, 2).Value = "x"
Cells(1, 3).Value = "y"
Cells(2, 1).Value = t
Cells(2, 2).Value = x
Cells(2, 3).Value = y
For i = 0 To 5000
K1 = F(t, x, y) * dt
L1 = G(t, x, y) * dt
K2 = F(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
L2 = G(t + dt / 2, x + K1 / 2, y + L1 / 2) * dt
K3 = F(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
L3 = G(t + dt / 2, x + K2 / 2, y + L2 / 2) * dt
K4 = F(t + dt, x + K3, y + L3) * dt
L4 = G(t + dt, x + K3, y + L3) * dt
t = t + dt
x = x + (K1 + 2 * K2 + 2 * K3 + K4) / 6
y = y + (L1 + 2 * L2 + 2 * L3 + L4) / 6
Cells(3 + i, 1).Value = t
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y
Next i
End Sub
Function F(t, x, y)
F = (8 - 3 * y) * x
End Function
Function G(t, x, y)
G = (-18 + 4 * x) * y
End Function
解析結果:

※特定のxに対してyは周期的に変化していることが確認できる。

※x、yの経時変化をみると図のようになっている。
このようにして、Runge-Kutta法を応用すると連立微分方程式のような
複雑な方程式も解析できます。
Runge-Kutta法とは、微分方程式の解法の一つです。
(原理の詳細:http://hooktail.org/computer/index.php?Runge-Kutta%CB%A1)
例えば、任意の微分方程式に対して、
dy/dx = f(x,y)に対して
k1 = f(x,y)
k2 = f(x+Δx/2,y+k1*Δx/2)
k3 = f(x+Δx/2,y+k2*Δx/2)
k4 = f(x+Δx,y+k3*Δx)
Δy = (Δx/6)*(k1+2k2+2k3+k4)
とすることでΔxに対するΔyを予想し、y=f(x)を正確に近似する方法です。
具体的にExcelのマクロを作って計算してみましょう。
問い:微分方程式dy/dx = xyをRunge-Kutta法で解け。ただし、x = 0ならy=10とする。
解法:上記計算のルールを用いてマクロをつくると下のようになる。
Sub RungeKutta()
Dim K1, K2, K3, K4 As Single
Dim x, y As Single
Dim dx, dy As Single
Dim i As Long
Cells(2, 2).Value = "x"
Cells(2, 3).Value = "y"
x = 0
y = 10
Cells(3, 2).Value = x
Cells(3, 3).Value = y
dx = 0.01
For i = 1 To 300
K1 = F(x, y)
K2 = F(x + dx / 2, y + dx / 2 * K1)
K3 = F(x + dx / 2, y + dx / 2 * K2)
K4 = F(x + dx, y + dx * K3)
dy = (K1 + 2 * K2 + 2 * K3 + K4) * (dx / 6)
x = x + dx
y = y + dy
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y
Next i
End Sub
Function F(x, y)
F = -2 * x * y
End Function
計算結果
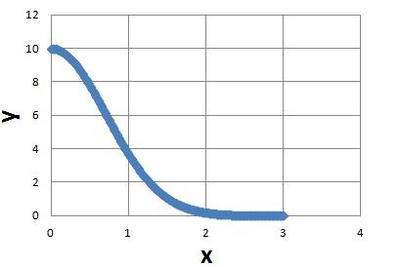
このような簡素なプログラミングでも微分方程式は精度よく計算できます。
とくに、Runge-Kutta法は常微分方程式であれば、
複雑な式でも解析が容易です。以後、Runge-Kutta法の解析例を
紹介していきたいと思います。
(原理の詳細:http://hooktail.org/computer/index.php?Runge-Kutta%CB%A1)
例えば、任意の微分方程式に対して、
dy/dx = f(x,y)に対して
k1 = f(x,y)
k2 = f(x+Δx/2,y+k1*Δx/2)
k3 = f(x+Δx/2,y+k2*Δx/2)
k4 = f(x+Δx,y+k3*Δx)
Δy = (Δx/6)*(k1+2k2+2k3+k4)
とすることでΔxに対するΔyを予想し、y=f(x)を正確に近似する方法です。
具体的にExcelのマクロを作って計算してみましょう。
問い:微分方程式dy/dx = xyをRunge-Kutta法で解け。ただし、x = 0ならy=10とする。
解法:上記計算のルールを用いてマクロをつくると下のようになる。
Sub RungeKutta()
Dim K1, K2, K3, K4 As Single
Dim x, y As Single
Dim dx, dy As Single
Dim i As Long
Cells(2, 2).Value = "x"
Cells(2, 3).Value = "y"
x = 0
y = 10
Cells(3, 2).Value = x
Cells(3, 3).Value = y
dx = 0.01
For i = 1 To 300
K1 = F(x, y)
K2 = F(x + dx / 2, y + dx / 2 * K1)
K3 = F(x + dx / 2, y + dx / 2 * K2)
K4 = F(x + dx, y + dx * K3)
dy = (K1 + 2 * K2 + 2 * K3 + K4) * (dx / 6)
x = x + dx
y = y + dy
Cells(3 + i, 2).Value = x
Cells(3 + i, 3).Value = y
Next i
End Sub
Function F(x, y)
F = -2 * x * y
End Function
計算結果
このような簡素なプログラミングでも微分方程式は精度よく計算できます。
とくに、Runge-Kutta法は常微分方程式であれば、
複雑な式でも解析が容易です。以後、Runge-Kutta法の解析例を
紹介していきたいと思います。
奇数を今度は次のように並べてみよう
1番目:1
2番目:3,5
3番目:7,9,11
4番目:13,15,17,19
規則性は理解できただろうか?
奇数列1,3,5,7,9,11,13,15,17,19…に対して
1番目の列は、奇数列の左から数字を1個取り出して1のみ
2番目の列は、先ほど取り出した1個を除き、奇数列の左から数字を2個取り出して3,5
…
といった具合で奇数を取り出しています。
前回と同じように、この和を見てみよう。
1番目:1 = 1 = 1×1×1
2番目:3+5 = 8 = 2×2×2
3番目:7+9+11 =27 = 3×3×3
4番目:13+15+17+19 = 64 =4×4×4
:
:
なんと、今度は3乗の数になっていました。
私は、このルールを発見した時、感動するとともに奇数は奇なる数と思いましたね。
この数列を利用して1^3+2^3+3^3+…+n^3を求めることが可能です。
n^3までの和は、1~n番目までの列に存在するすべての奇数の和と同じです。
また数列のルールにもどると、1からスタートして奇数列から
1+2+3+4+…+n個の奇数を取り出しています。
よってpart1より、奇数列の和は足した個数の二乗になるので
1^3+2^3+3^3+…+n^3 =(1+2+3+4+…+n)^2となることが容易に確認できるでしょう。
詳細:奇数を並べると-part1
こういう方法を用いても高校数学の数列の公式をつくることができるのです。
1番目:1
2番目:3,5
3番目:7,9,11
4番目:13,15,17,19
規則性は理解できただろうか?
奇数列1,3,5,7,9,11,13,15,17,19…に対して
1番目の列は、奇数列の左から数字を1個取り出して1のみ
2番目の列は、先ほど取り出した1個を除き、奇数列の左から数字を2個取り出して3,5
…
といった具合で奇数を取り出しています。
前回と同じように、この和を見てみよう。
1番目:1 = 1 = 1×1×1
2番目:3+5 = 8 = 2×2×2
3番目:7+9+11 =27 = 3×3×3
4番目:13+15+17+19 = 64 =4×4×4
:
:
なんと、今度は3乗の数になっていました。
私は、このルールを発見した時、感動するとともに奇数は奇なる数と思いましたね。
この数列を利用して1^3+2^3+3^3+…+n^3を求めることが可能です。
n^3までの和は、1~n番目までの列に存在するすべての奇数の和と同じです。
また数列のルールにもどると、1からスタートして奇数列から
1+2+3+4+…+n個の奇数を取り出しています。
よってpart1より、奇数列の和は足した個数の二乗になるので
1^3+2^3+3^3+…+n^3 =(1+2+3+4+…+n)^2となることが容易に確認できるでしょう。
詳細:奇数を並べると-part1
こういう方法を用いても高校数学の数列の公式をつくることができるのです。
[1]
[2]


