理系の若者が思ったことを書くブログです。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
京都市立芸術大学 の藤原隆男のHPを参考にすると
土壌中放射線物質によって人間に暴露される放射線の強さを計算できます。
詳細:http://kcua.ac.jp/~fujiwara/nuclear/air_dose.html
前回の日記で紹介した台形公式のロジックをもとに、数値積分法を応用して
土壌からの放射線の強さを計算するプログラミングを作ってみようと思う。
まず、上記のHPより放射線の強さの式は:
I =∫(0~∞) p*exp(-u*√(r^2 + h^2))*(2π*r*dr)/{4π(r^2 + h^2)}
I =p*∫(0~∞) exp(-u*√(r^2 + h^2))*(r*dr)/{2*(r^2 + h^2)}
となります。これを計算してSvに換算できれば土壌による放射線のリスクを
正確に評価できます。本稿では、Iの計算方法まで論じます。
さて、25℃の大気では、u = 1/110.16 m^2であり、
p=1のときのIを計算すると次のプログラムを実行すればいいでしょう。
Sub intensity_calc()
Dim R As Double
Dim dR As Double
Dim U As Double
Dim A, B As Double
Dim P, Q As Double
H = 0.001
S = 0
U = 1 / 110
dR = 0.01
Cells(2, 2).Value = "h"
Cells(2, 3).Value = "I"
For i = 1 To 200
S = 0
R = 0
'台形公式計算
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR * 0.5
R = R + dR
For j = 1 To 10000
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR
R = R + dR
Next j
S = S - (A / B) * R * dR * 0.5
Cells(2 + i, 2).Value = H
Cells(2 + i, 3).Value = S
H = H + 0.1
Next i
End Sub
解析結果:
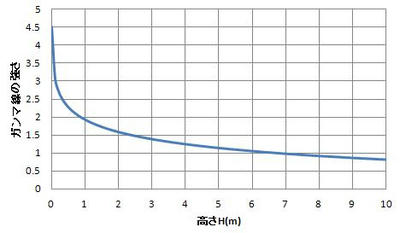
この図は紹介したHPにも載っていますが、数学的な導出がありません。
理論的には、こういった計算を行えば解析できるということを
このブログで示しました。この解析結果をそのまま読みとめれば、
土壌のBq/m2から、高さあたりの被ばく量を概算できるのです。
次回は、土壌中のBq/m2とSvの関係を評価します。
土壌中放射線物質によって人間に暴露される放射線の強さを計算できます。
詳細:http://kcua.ac.jp/~fujiwara/nuclear/air_dose.html
前回の日記で紹介した台形公式のロジックをもとに、数値積分法を応用して
土壌からの放射線の強さを計算するプログラミングを作ってみようと思う。
まず、上記のHPより放射線の強さの式は:
I =∫(0~∞) p*exp(-u*√(r^2 + h^2))*(2π*r*dr)/{4π(r^2 + h^2)}
I =p*∫(0~∞) exp(-u*√(r^2 + h^2))*(r*dr)/{2*(r^2 + h^2)}
となります。これを計算してSvに換算できれば土壌による放射線のリスクを
正確に評価できます。本稿では、Iの計算方法まで論じます。
さて、25℃の大気では、u = 1/110.16 m^2であり、
p=1のときのIを計算すると次のプログラムを実行すればいいでしょう。
Sub intensity_calc()
Dim R As Double
Dim dR As Double
Dim U As Double
Dim A, B As Double
Dim P, Q As Double
H = 0.001
S = 0
U = 1 / 110
dR = 0.01
Cells(2, 2).Value = "h"
Cells(2, 3).Value = "I"
For i = 1 To 200
S = 0
R = 0
'台形公式計算
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR * 0.5
R = R + dR
For j = 1 To 10000
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR
R = R + dR
Next j
S = S - (A / B) * R * dR * 0.5
Cells(2 + i, 2).Value = H
Cells(2 + i, 3).Value = S
H = H + 0.1
Next i
End Sub
解析結果:
この図は紹介したHPにも載っていますが、数学的な導出がありません。
理論的には、こういった計算を行えば解析できるということを
このブログで示しました。この解析結果をそのまま読みとめれば、
土壌のBq/m2から、高さあたりの被ばく量を概算できるのです。
次回は、土壌中のBq/m2とSvの関係を評価します。
PR
ここでは、100nmのホールからセシウムが流出する質量損失速度を計算してみる。(前回の日記参照)
はじめに、小さな孔の上は真空であるとし、セシウムが十分多量にあることでセシウム蒸気の供給が順次行われるものとする。
※実際は、真空ではない。真空と仮定すると流出量が大きくなることに注意。また、十分な蒸気の供給があるということは、蒸気圧PはdP/dt = 0となり、環境温度に対して一定である。極端な条件であるが、極端な条件よりは実際の質量損失量が小さいので、まずは極端な条件を把握し、どれだけ小さな値になるか理解することが大事である。
この場合のセシウム流出量は、分子運動論によると衝突頻度×面積×原子質量で計算できる。したがって、
Δm/Δt = m*Zw*A0…①
となる。ここで、mはセシウム原子1つの重量、Zwは衝突頻度、A0はホール面積とする。グレアムの流出の法則より、流出速度vは一般的に次式のようになる。
v=A0*Zw = A0*p*NA/(2π*MRT)^0.5 …②
pはセシウムの蒸気圧、NAはアボガドロ定数、Mは原子量、Rは気体定数、Tは環境温度とする。結局、①、②より次式によって流出挙動を考えることができる。
Δm/Δt = (M/NA) * p*NA/(2π*MRT)^0.5 *A0
Δm/Δt = p*A0*(M/(2π*RT))^0.5 …③
このpは、アントワンの式によって記述できる。セシウムのアントワン定数は こちらの日記を参考にしよう。定数をそれぞれ計算すると
p = 10^(8.8394 - 3615.1/(200+259.56)) = 9.396 [Pa]
A0 = (50/10^9)^2*3.141592 = 7.854 × 10^-15 [m2]
M = 0.1329 [kg/mol]
R = 8.314 [J/K/mol]
T = 200+273 = 473[K]
Δm/Δt = 9.396*7.854*10^-15*(0.1329/(2*3.141592*8.314*473))^0.5
Δm/Δt = 1.71 × 10^-16 [kg/s] = 0.17 [ng/s]
つまり、ホールから1秒当たり0.17ナノグラムしかセシウムは流出しえない。
※ナノグラムは1gの1/1,000,000,000です。
Δm/Δt < 0.17 ng/sであるのはいうまでもなく、直径を根拠にバグフィルターから流出するという議論はミスリーディングではないだろうか?
この計算結果は、どう理解すればいいか? つまり、セシウムが二百℃では固体状態で存在するため、蒸気圧が低くなり、100ナノメートルのホールがあっても流出しないのである。
はじめに、小さな孔の上は真空であるとし、セシウムが十分多量にあることでセシウム蒸気の供給が順次行われるものとする。
※実際は、真空ではない。真空と仮定すると流出量が大きくなることに注意。また、十分な蒸気の供給があるということは、蒸気圧PはdP/dt = 0となり、環境温度に対して一定である。極端な条件であるが、極端な条件よりは実際の質量損失量が小さいので、まずは極端な条件を把握し、どれだけ小さな値になるか理解することが大事である。
この場合のセシウム流出量は、分子運動論によると衝突頻度×面積×原子質量で計算できる。したがって、
Δm/Δt = m*Zw*A0…①
となる。ここで、mはセシウム原子1つの重量、Zwは衝突頻度、A0はホール面積とする。グレアムの流出の法則より、流出速度vは一般的に次式のようになる。
v=A0*Zw = A0*p*NA/(2π*MRT)^0.5 …②
pはセシウムの蒸気圧、NAはアボガドロ定数、Mは原子量、Rは気体定数、Tは環境温度とする。結局、①、②より次式によって流出挙動を考えることができる。
Δm/Δt = (M/NA) * p*NA/(2π*MRT)^0.5 *A0
Δm/Δt = p*A0*(M/(2π*RT))^0.5 …③
このpは、アントワンの式によって記述できる。セシウムのアントワン定数は こちらの日記を参考にしよう。定数をそれぞれ計算すると
p = 10^(8.8394 - 3615.1/(200+259.56)) = 9.396 [Pa]
A0 = (50/10^9)^2*3.141592 = 7.854 × 10^-15 [m2]
M = 0.1329 [kg/mol]
R = 8.314 [J/K/mol]
T = 200+273 = 473[K]
Δm/Δt = 9.396*7.854*10^-15*(0.1329/(2*3.141592*8.314*473))^0.5
Δm/Δt = 1.71 × 10^-16 [kg/s] = 0.17 [ng/s]
つまり、ホールから1秒当たり0.17ナノグラムしかセシウムは流出しえない。
※ナノグラムは1gの1/1,000,000,000です。
Δm/Δt < 0.17 ng/sであるのはいうまでもなく、直径を根拠にバグフィルターから流出するという議論はミスリーディングではないだろうか?
この計算結果は、どう理解すればいいか? つまり、セシウムが二百℃では固体状態で存在するため、蒸気圧が低くなり、100ナノメートルのホールがあっても流出しないのである。
http://ooruri777.seesaa.net/article/269354790.html
>バグフィルターが100nm(ナノミリ)しか無いと分かると、「気化したセシウム(0.5nm)を99.99%も除去することは不可能だ」 と直ぐに分かります。
バグフィルターのメーカーに問い合わせても、「放射性物質の除去は考慮していない」 と当たり前の返答が返ってきます。法的に基準が無いからです。
こういう意見をある確率で見ますね。
正直、もう少し定量的に考えないと問題の本質はみえてきません。
そこで思考実験してみましょう。下の図をみてください。
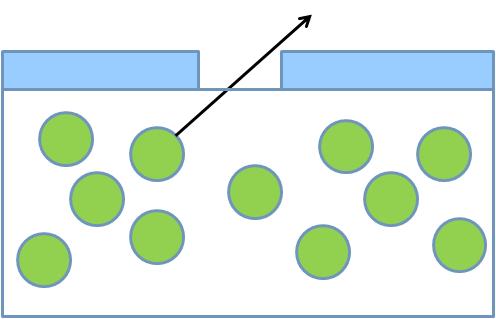
緑のボールは、気化したセシウム粒子を表します(200度だとセシウムの沸点には到達していないが、蒸気圧が零になることはないので、こういったセシウムがホールを透過しうる。)
このセシウム粒子が実際の温度環境下で100nmのホールを矢印のように
透過する運動を考えます。この運動の平均速度が計算できれば
分子運動論に基づくセシウムの流出状況を想像できるでしょう。
次回の日記では、この運動について分子運動という物理化学の
原理に基づいて計算したいと思います。皆様も考えてみてください。
※ヒント:前回の日記
それでは失礼します。
>バグフィルターが100nm(ナノミリ)しか無いと分かると、「気化したセシウム(0.5nm)を99.99%も除去することは不可能だ」 と直ぐに分かります。
バグフィルターのメーカーに問い合わせても、「放射性物質の除去は考慮していない」 と当たり前の返答が返ってきます。法的に基準が無いからです。
こういう意見をある確率で見ますね。
正直、もう少し定量的に考えないと問題の本質はみえてきません。
そこで思考実験してみましょう。下の図をみてください。
緑のボールは、気化したセシウム粒子を表します(200度だとセシウムの沸点には到達していないが、蒸気圧が零になることはないので、こういったセシウムがホールを透過しうる。)
このセシウム粒子が実際の温度環境下で100nmのホールを矢印のように
透過する運動を考えます。この運動の平均速度が計算できれば
分子運動論に基づくセシウムの流出状況を想像できるでしょう。
次回の日記では、この運動について分子運動という物理化学の
原理に基づいて計算したいと思います。皆様も考えてみてください。
※ヒント:前回の日記
それでは失礼します。
例えば、瓦礫を焼却する場合、セシウムは焼却炉中で蒸気としても存在しうる。
そこで、Antoineの式を用いてセシウムの蒸気圧を決定する。
Antoineの式とは、蒸気圧における経験則であり、概要は下記URL参照のこと。
http://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%B3%E3%83%88%E3%83%AF%E3%83%B3%E5%BC%8F
この式の定義より、セシウムの蒸気圧P[Pa]は、温度T[℃]に対して次式のようになる。
LogP = A - B/(T+C) …(1)
ここで、A,B,Cはアントワン定数である。この式を変形すると、
(1)⇔(T+C)LogP = A(T+C) - B
⇔TLogP + CLogP = AT + AC - B
⇔AT + (A - LogP)C - B - TLogP = 0…(2)
のようになる。(2)式に実測値を代入しよう。
(データ元:http://blog.livedoor.jp/toshi_tomie/archives/51935330.html)
T = 22なら、 P = 10^-4 なので
22A + (A + 4)C - B + 88 = 0 …(3)
T = 269なら、P = 100 なので
269A + (A - 2)C - B - 538 = 0 …(4)
T = 682なら、P = 10000なので
682A + (A - 5)C - B - 3410 = 0 …(5)
となる。(3)~(5)より、A,B,Cを決定すると、
(4) - (3)⇔247A - 6C - 626 = 0
(247*3)*A - 18C - (626*3) = 0
(5) - (3)⇔660A - 9C - 3498 = 0
⇔(660*2)*A - 18C - (3498*2) = 0
A = (3498*2 - 626*3)/(660*2 - 247*3) = 8.8394
C = (660*8.8394 - 3498)/9 = 259.56
B = 22*8.8394+(8.8394+4)*259.56 + 88 = 3615.1
LogP = 8.8394 - 3615.1/(T+259.56)
P = 10^(8.8394 - 3615.1/(T+259.56)) …(6)
が得られる。この式によってセシウム蒸気圧の予測が可能となる。
そこで、Antoineの式を用いてセシウムの蒸気圧を決定する。
Antoineの式とは、蒸気圧における経験則であり、概要は下記URL参照のこと。
http://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%B3%E3%83%88%E3%83%AF%E3%83%B3%E5%BC%8F
この式の定義より、セシウムの蒸気圧P[Pa]は、温度T[℃]に対して次式のようになる。
LogP = A - B/(T+C) …(1)
ここで、A,B,Cはアントワン定数である。この式を変形すると、
(1)⇔(T+C)LogP = A(T+C) - B
⇔TLogP + CLogP = AT + AC - B
⇔AT + (A - LogP)C - B - TLogP = 0…(2)
のようになる。(2)式に実測値を代入しよう。
(データ元:http://blog.livedoor.jp/toshi_tomie/archives/51935330.html)
T = 22なら、 P = 10^-4 なので
22A + (A + 4)C - B + 88 = 0 …(3)
T = 269なら、P = 100 なので
269A + (A - 2)C - B - 538 = 0 …(4)
T = 682なら、P = 10000なので
682A + (A - 5)C - B - 3410 = 0 …(5)
となる。(3)~(5)より、A,B,Cを決定すると、
(4) - (3)⇔247A - 6C - 626 = 0
(247*3)*A - 18C - (626*3) = 0
(5) - (3)⇔660A - 9C - 3498 = 0
⇔(660*2)*A - 18C - (3498*2) = 0
A = (3498*2 - 626*3)/(660*2 - 247*3) = 8.8394
C = (660*8.8394 - 3498)/9 = 259.56
B = 22*8.8394+(8.8394+4)*259.56 + 88 = 3615.1
LogP = 8.8394 - 3615.1/(T+259.56)
P = 10^(8.8394 - 3615.1/(T+259.56)) …(6)
が得られる。この式によってセシウム蒸気圧の予測が可能となる。
バナナ100gあたりのカリウム含有量は360mg = 0.36 gである。
自然界に存在するカリウムの0.0117パーセントが放射性同位体のカリウム40であり、
1本150g程度のバナナは、0.36×0.0117/100 *150/100= 6.318× 10^-5 g
の放射性カリウム40を含有していることが確認できる。
放射能の強さは、これまでの日記から
|dN/dt| = λN = (Log(2)/T)*N0
|dN/dt|= 0.69315/(1.28*10^9*365*24*3600)*(6.318*10^-5/40*6.02*10^23)
|dN/dt|= 16.3 Bq
つまり、自然界のバナナは原発事故と関係なく16.3Bqの放射能をおびています。
これに実効線量係数というものをかければSvに換算できます。すなわち、
16.3*6.2*10^-9 = 1.01× 10^-7 = 0.101 μSv
結論:原発事故とか関係なく自然界に存在するバナナ1本を食べると
0.101μSVの被ばくをするだろう。
こういう定量感覚を持ってニュースを見たほうがい。では宿題。
バナナは危険か危険でないか?
自然界に存在するカリウムの0.0117パーセントが放射性同位体のカリウム40であり、
1本150g程度のバナナは、0.36×0.0117/100 *150/100= 6.318× 10^-5 g
の放射性カリウム40を含有していることが確認できる。
放射能の強さは、これまでの日記から
|dN/dt| = λN = (Log(2)/T)*N0
|dN/dt|= 0.69315/(1.28*10^9*365*24*3600)*(6.318*10^-5/40*6.02*10^23)
|dN/dt|= 16.3 Bq
つまり、自然界のバナナは原発事故と関係なく16.3Bqの放射能をおびています。
これに実効線量係数というものをかければSvに換算できます。すなわち、
16.3*6.2*10^-9 = 1.01× 10^-7 = 0.101 μSv
結論:原発事故とか関係なく自然界に存在するバナナ1本を食べると
0.101μSVの被ばくをするだろう。
こういう定量感覚を持ってニュースを見たほうがい。では宿題。
バナナは危険か危険でないか?
[1]
[2]


