理系の若者が思ったことを書くブログです。
×
[PR]上記の広告は3ヶ月以上新規記事投稿のないブログに表示されています。新しい記事を書く事で広告が消えます。
①山ほど書類仕事がある。
②私は首席で卒業しました。
③それで?
④引き受けるよ。
⑤(レストランで6番テーブルが上がった時に)6番上がりだ。
⑥ベルトを締めろ。
⑦あなたって本当に鈍い男ね
①I've got tons of paperwork.
②I graduated with honors.
③Go on.
④I am in(例:He is in computer⇒彼はコンピュータの仕事をしている)
⑤Six is up.(例:Tea 's up)
⑥Fasten your seatbelt
⑦You're really not getting this.
http://www.eonet.ne.jp/~syumi-eigo/meninblack.html
PR
素数とは、1 と自分自身以外に正の約数を持たない、1 でない自然数のことです。
1~100までの素数は容易に探索できるかもしれません。
でも1~1000までの素数となるとちょっと骨が折れるでしょうね。
そこで、プログラミングの出番です。
実を言うと素数を探索するアルゴリズムは複数あります。
したがって、素数はコンピュータ計算でも探索できます。
ここでは、次の方法で素数を探索してみようと思います。
① a_k = k (k = 1,2,3…1000)となる数列akを定義する。
② k = 1であれば、素数ではないと判断する。
③ k = 2であれば、素数と判断する。
③ k >2であるa_kを2~kまでのすべての数で割っていく。
④ ③のときに、割った数pに対してひとつでもa_k ≡ 0 (mod p) を満たせば
素数でないと判断する。
※modの意味がわからない方はこちらへ⇒http://sur.ac/faq/mod.html
⑤ kの値を繰り上げて③~④を繰り返す。
上の計算方法をVBAプログラムにすると次のようになります。
Sub primenumber()
Dim k, j As Long
Dim hantei As Long
Dim counter As Long
counter = 0
For k = 1 To 1000
If k = 1 Then
hantei = 0
'1は素数じゃない。
End If
If k = 2 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'2は素数である。
End If
If k = 3 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'3は素数である。
End If
If k > 3 Then
hantei = 1
For j = 2 To k - 1
Data = k Mod j
If Data = 0 Then
hantei = 0
End If
Next j
If hantei = 1 Then
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
End If
'3以上の数の素数判定実施。
End If
Next k
End Sub
解析結果:
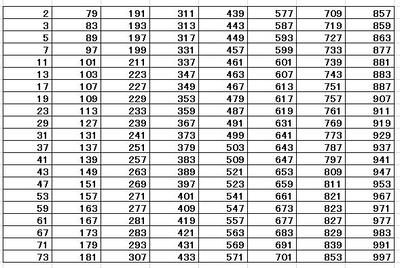
このように、プログラミングを勉強すれば素数も簡単に探せるようになるのです。
1~100までの素数は容易に探索できるかもしれません。
でも1~1000までの素数となるとちょっと骨が折れるでしょうね。
そこで、プログラミングの出番です。
実を言うと素数を探索するアルゴリズムは複数あります。
したがって、素数はコンピュータ計算でも探索できます。
ここでは、次の方法で素数を探索してみようと思います。
① a_k = k (k = 1,2,3…1000)となる数列akを定義する。
② k = 1であれば、素数ではないと判断する。
③ k = 2であれば、素数と判断する。
③ k >2であるa_kを2~kまでのすべての数で割っていく。
④ ③のときに、割った数pに対してひとつでもa_k ≡ 0 (mod p) を満たせば
素数でないと判断する。
※modの意味がわからない方はこちらへ⇒http://sur.ac/faq/mod.html
⑤ kの値を繰り上げて③~④を繰り返す。
上の計算方法をVBAプログラムにすると次のようになります。
Sub primenumber()
Dim k, j As Long
Dim hantei As Long
Dim counter As Long
counter = 0
For k = 1 To 1000
If k = 1 Then
hantei = 0
'1は素数じゃない。
End If
If k = 2 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'2は素数である。
End If
If k = 3 Then
hantei = 1
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
'3は素数である。
End If
If k > 3 Then
hantei = 1
For j = 2 To k - 1
Data = k Mod j
If Data = 0 Then
hantei = 0
End If
Next j
If hantei = 1 Then
counter = counter + 1
Cells(counter, 1).Value = counter
Cells(counter, 2).Value = k
End If
'3以上の数の素数判定実施。
End If
Next k
End Sub
解析結果:
このように、プログラミングを勉強すれば素数も簡単に探せるようになるのです。
京都市立芸術大学 の藤原隆男のHPを参考にすると
土壌中放射線物質によって人間に暴露される放射線の強さを計算できます。
詳細:http://kcua.ac.jp/~fujiwara/nuclear/air_dose.html
前回の日記で紹介した台形公式のロジックをもとに、数値積分法を応用して
土壌からの放射線の強さを計算するプログラミングを作ってみようと思う。
まず、上記のHPより放射線の強さの式は:
I =∫(0~∞) p*exp(-u*√(r^2 + h^2))*(2π*r*dr)/{4π(r^2 + h^2)}
I =p*∫(0~∞) exp(-u*√(r^2 + h^2))*(r*dr)/{2*(r^2 + h^2)}
となります。これを計算してSvに換算できれば土壌による放射線のリスクを
正確に評価できます。本稿では、Iの計算方法まで論じます。
さて、25℃の大気では、u = 1/110.16 m^2であり、
p=1のときのIを計算すると次のプログラムを実行すればいいでしょう。
Sub intensity_calc()
Dim R As Double
Dim dR As Double
Dim U As Double
Dim A, B As Double
Dim P, Q As Double
H = 0.001
S = 0
U = 1 / 110
dR = 0.01
Cells(2, 2).Value = "h"
Cells(2, 3).Value = "I"
For i = 1 To 200
S = 0
R = 0
'台形公式計算
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR * 0.5
R = R + dR
For j = 1 To 10000
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR
R = R + dR
Next j
S = S - (A / B) * R * dR * 0.5
Cells(2 + i, 2).Value = H
Cells(2 + i, 3).Value = S
H = H + 0.1
Next i
End Sub
解析結果:
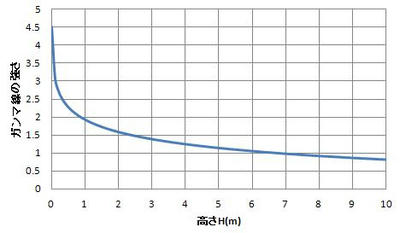
この図は紹介したHPにも載っていますが、数学的な導出がありません。
理論的には、こういった計算を行えば解析できるということを
このブログで示しました。この解析結果をそのまま読みとめれば、
土壌のBq/m2から、高さあたりの被ばく量を概算できるのです。
次回は、土壌中のBq/m2とSvの関係を評価します。
土壌中放射線物質によって人間に暴露される放射線の強さを計算できます。
詳細:http://kcua.ac.jp/~fujiwara/nuclear/air_dose.html
前回の日記で紹介した台形公式のロジックをもとに、数値積分法を応用して
土壌からの放射線の強さを計算するプログラミングを作ってみようと思う。
まず、上記のHPより放射線の強さの式は:
I =∫(0~∞) p*exp(-u*√(r^2 + h^2))*(2π*r*dr)/{4π(r^2 + h^2)}
I =p*∫(0~∞) exp(-u*√(r^2 + h^2))*(r*dr)/{2*(r^2 + h^2)}
となります。これを計算してSvに換算できれば土壌による放射線のリスクを
正確に評価できます。本稿では、Iの計算方法まで論じます。
さて、25℃の大気では、u = 1/110.16 m^2であり、
p=1のときのIを計算すると次のプログラムを実行すればいいでしょう。
Sub intensity_calc()
Dim R As Double
Dim dR As Double
Dim U As Double
Dim A, B As Double
Dim P, Q As Double
H = 0.001
S = 0
U = 1 / 110
dR = 0.01
Cells(2, 2).Value = "h"
Cells(2, 3).Value = "I"
For i = 1 To 200
S = 0
R = 0
'台形公式計算
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR * 0.5
R = R + dR
For j = 1 To 10000
A = Exp(-U * (R ^ 2 + H ^ 2) ^ 0.5)
B = 2 * (R ^ 2 + H ^ 2)
S = S + (A / B) * R * dR
R = R + dR
Next j
S = S - (A / B) * R * dR * 0.5
Cells(2 + i, 2).Value = H
Cells(2 + i, 3).Value = S
H = H + 0.1
Next i
End Sub
解析結果:
この図は紹介したHPにも載っていますが、数学的な導出がありません。
理論的には、こういった計算を行えば解析できるということを
このブログで示しました。この解析結果をそのまま読みとめれば、
土壌のBq/m2から、高さあたりの被ばく量を概算できるのです。
次回は、土壌中のBq/m2とSvの関係を評価します。
PART1はあくまで台形公式についてのみ書きます。
今、y = x^2を0から1の範囲で積分せよという問題を考える。
この積分は簡単だと思う。何故なら、∫x^2dx =x^3/3+Cより、
1/3だとすぐ確認できるからである。
では、y=√(x^4-x+sinx)に変更するとどうだろうか?
こういう式になった途端にどうすればいいかわからなくなるだろう。
このように、数学的にちゃんと積分する方法がわからない式だってたくさんある。
しかし、y=f(x)がどんな式であれ、近似的に精度よく積分できる方法も存在する。
台形公式は、そういった手法の一つである。台形公式は、
積分範囲を何点かに分割して台形をつくり、その台形の面積を求めることで
数値積分する方法である。
具体例:今、y=f(x)をa~b( a
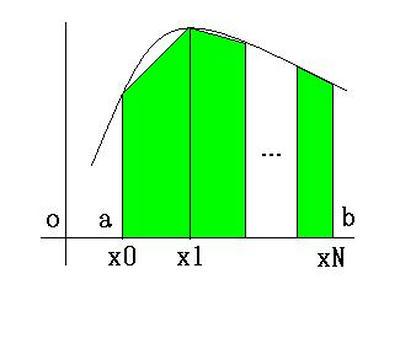
この図から台形の面積の総和Stを調べると、数学的に下記の式であらわせる。
St = {(f(x0)+f(x1))*(x1-x0)/2}+…+{(f(xN)+f(xN-1))*(xN-xN-1)/2}…(1)
今分割をx1-x0 = x2 - x1 = …xk+1-xk = xN - x0 = hとなるように行うのであれば、
St = {f(x0) + f(xN)}/2*h + Σf(xk)*h/2 (k=1 ~ k = N-1)…(2)
がなりたつ。分割数を増やしていけば、この台形の面積の総和は積分結果に近づく。
この(2)式を実行するプログラミングとf(x)を定義すれば、
どんな式でも簡単に積分できるようになるでしょう。
今、y = x^2を0から1の範囲で積分せよという問題を考える。
この積分は簡単だと思う。何故なら、∫x^2dx =x^3/3+Cより、
1/3だとすぐ確認できるからである。
では、y=√(x^4-x+sinx)に変更するとどうだろうか?
こういう式になった途端にどうすればいいかわからなくなるだろう。
このように、数学的にちゃんと積分する方法がわからない式だってたくさんある。
しかし、y=f(x)がどんな式であれ、近似的に精度よく積分できる方法も存在する。
台形公式は、そういった手法の一つである。台形公式は、
積分範囲を何点かに分割して台形をつくり、その台形の面積を求めることで
数値積分する方法である。
具体例:今、y=f(x)をa~b( a
この図から台形の面積の総和Stを調べると、数学的に下記の式であらわせる。
St = {(f(x0)+f(x1))*(x1-x0)/2}+…+{(f(xN)+f(xN-1))*(xN-xN-1)/2}…(1)
今分割をx1-x0 = x2 - x1 = …xk+1-xk = xN - x0 = hとなるように行うのであれば、
St = {f(x0) + f(xN)}/2*h + Σf(xk)*h/2 (k=1 ~ k = N-1)…(2)
がなりたつ。分割数を増やしていけば、この台形の面積の総和は積分結果に近づく。
この(2)式を実行するプログラミングとf(x)を定義すれば、
どんな式でも簡単に積分できるようになるでしょう。


