温暖化については、色々な言説がある。
嘘だという言説も面白いのかもしれない。
厳しい意見を述べるけれども、
うそと決めつけるロジックが稚拙だと思う。

例えば、東京大学のサステイナビリティ学に関するHPでは、
温暖化の懐疑論に関する意見がまとめられている。

http://www.ir3s.u-tokyo.ac.jp/sosho

こちらのHPを読む限りでは、温暖化が嘘だという
言説もいまいちだなと思う。

もちろん、温暖化が嘘という言論をすべて否定するつもりもないが、
最低限、科学的な方法にのっとった主張をすべきであり、
明らかにミスリーディングな考察が多すぎるのではないか？

[2回]

前回、溶媒の粘度をη0、溶液の粘度をηとして、
オストワルドの粘度計の原理を示した。

今日は固有粘度について語ろうと思う。

溶液の溶質の濃度をCとすると、実はηとη0の間には、一般的に

η = η0(1+[η]C+[η2]C^2+…)…(1)

が成り立ち、状態方程式をビリアル展開した式に似た近似式が成り立つ。

よって、高分子溶液のようにCが十分に小さい場合、
C^2<<1なので、C^2≒0と近似してよい。この場合、

η = η0(1+[η]C)⇔[η]= {(η-η0)/η0}/C より[η]は次式のようになる。

∴　[η]　 =　Lim{C⇒0}　(η/η0 - 1)/C　…(2)

このような[η]のことを固有粘度と呼ぶ。
固有粘度は、Huggins Plotというデータ解析で解析することができる。

これは、Cに対して(η/η0-1)/Cをプロットすることで固有粘度を解析する方法である。

例えば、下表にEXCELでポリスチレン-トルエン溶液を用いて
(η/η0-1)/Cを解析した例を記す。



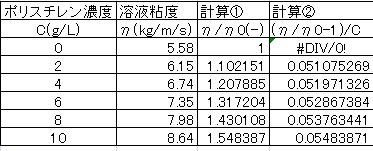
この表に対して、ポリスチレン濃度と計算②をプロットしたものがHuggins Plotであり、
Excelでグラフ化すると図のようになる。



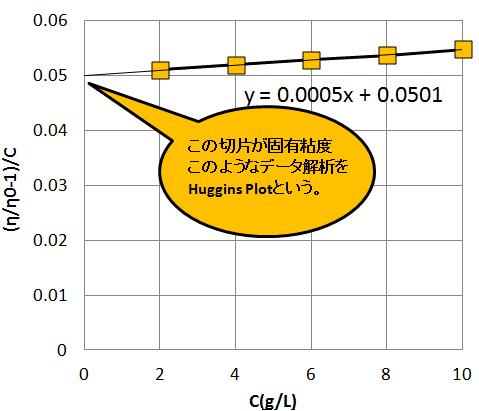
グラフの切片は、Lim{C⇒0}　(η/η0 - 1)/Cと同じであり、

固有粘度[η]は、[η]=0.0501となっていることが確認できた。

実験的にはこのようにして固有粘度を求められる。

[9回]

趣味の勉強日記です。

オストワルドの粘度計とは、下記動画で紹介されているガラス器具であり、
Ostwald　viscometerともいいます。



この器具は、溶液の粘度測定で幅広く利用されます。
英語で何を言ってるか分からない方のために図を用意しました。
詳細は下記をご覧ください。



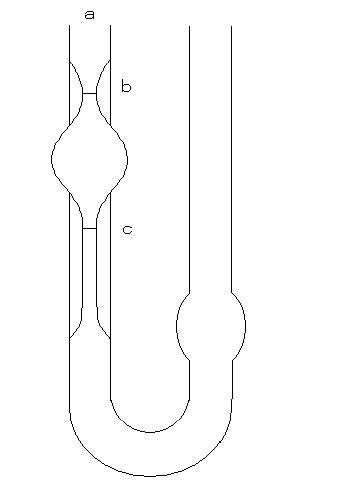
はじめに、右側から液体を入れます。注意してほしいのですが、
粘度測定を正確に行うなら恒温槽内で行いましょう。
次にa部にゴム管等をつけて溶液をb部まで吸い上げます。
温度が安定したところで、aを開放し液体を自由落下させます。
その際に液体がbからc部を通過する時間Δtをストップウォッチで測定することで
粘度を導くことが可能になるのです。なぜでしょうか？

はじめに、b部まで液体を吸い上げる際の圧力ΔPを計算しましょう。
このときの圧力変化ΔPは、ニュートンの運動方程式より導くことが可能であり、

ΔP = mg/S = ρgV/S = ρg(S・h)/S = ρgh…(1)
m…吸い上げた液体の質量
g…重力定数
S…bからc部までの平均断面積
V…bからc部の体積
h…bからc部までの高さ
ρ…液体の密度
となります。この流体の運動をハーゲンポアズイユの式で近似すると、

V/Δt = (πR^4/8η)*ΔP/h…(2)
を得ることができます。ここで、Rはb からcまでの容器断面における平均半径とします。(1)を(2)に代入すると、

η=(πρgR^4h)Δt/(8h)=ρAΔt　…(3)※A　= (πgR^4h)/(8h)であり定数

となり、粘度という物理量は非常にシンプルな関数で表現できました。

ふつう、溶媒の粘度をη0、溶液の粘度をηとして相対的に粘度を求めることが多いです。
なぜかというと、Aを決定しなくて済むからです。
上の式を考えればわかるけれども、溶媒の密度をρ0、落下時間をΔt0、
溶液の密度をρ、落下時間をΔtとすると

η0　=　A*ρ0*Δt0　…(4)
η　　=　A*ρ*Δt　…(5)
が導けます。(4)および(5)式からAを消去すると、

η/η0 = (ρ/ρ0)*(Δt/Δt0)…(6)

のような式を得ることができます。このη/η0 を相対粘度といいます。
オストワルドの粘度計は、このような相対粘度の解析に大変すぐれた
装置です。

[25回]